频繁项集算法 Apriori & FP-Growth
问题与数据介绍
问题
计算数据集的频繁项集并找出关联规则.
比较计算频繁项集的不同算法之间的时空复杂度.
发现关联规则之间的某些规律并讨论.
数据集
共有两组数据集
- Groceries: 购买物品
- Unix: 用户在 terminal 中使用的指令
算法介绍
Apriori
Apriori 算法基于先验规则: k 长度的频繁项集的所有 k-1 长度的子集也都是频繁项集. 从长度为 1 的频繁项集一直向上寻找.
算法改进
在第一次扫描数据的时候, 就将那些项包含哪些元素全部记录在 bitarray 中, 当进行筛选是否满足最小置信度的时候直接统计项中每个元素的 bitarray 进行与操作, 再统计其中 1 的个数即可知道是否符合最小支持度.
通过这一操作, 即可将原来时间复杂度为 m * k * n * p , 占用了算法大部分时间的过滤过程(k 为当前正在过滤的项集的长度, m 为长度为 k 的候选频繁项数量, n 为所有的项集数量, p 为项集的平均长度), 降为 m * k * n, 且其中遍历 n 的时间复杂度降低了非常多(原先需要读取项集的元素, 而优化后只需统计 01 即可)
代码实现基于 Efficient Apriori 并进行了以上的算法修改, 优化了过滤支持度的效率.
构建 bitarray, 统计包含每个元素的所有项集. 在之后根据阈值进行删除时效率更高.
join: 将长度为 k 的项集进行排序后, 从之归并出长度为 k+1 的项集.
prune: 遍历生成的长度为 k+1 的项集, 若其有长度为 k 的子集不属于原项集, 则剪去.
过滤: 遍历生成的新项集, 通过 bitarray 与计算, 得到包含当前项集的的原项集数量, 将数量小于最小支持度的项集过滤.
FP-Growth
代码实现基于 pyFP-growth 实现并进行了修改.
遍历频繁项, 将频繁项结果排序并取出满足最小支持度的频繁项.
遍历项集, 构建 FP-Tree. 判断: 树只有一条路径
若只有一条路径: 则其除了第一个元素的所有子集与第一个元素进行连接, 即为频繁项集.
否则: 对当前树的所有频繁项进行遍历, 并逐项从树中挖取, 构造新的频繁树, 重复判断是否只有一条路径. 直到提取出树的所有单条路径.
方法
比较
通过 CProfile 工具能够比较方便地对算法的时空复杂度进行分析.
记录数据
通过重载输出的记录值的 __repr__ 函数, 方便地打印并输出结果.
结果与分析
以下首先展示频繁项集的实验结果.
Groceries
在最小支持度为 0.05, 最小置信度为 0.2 情况下
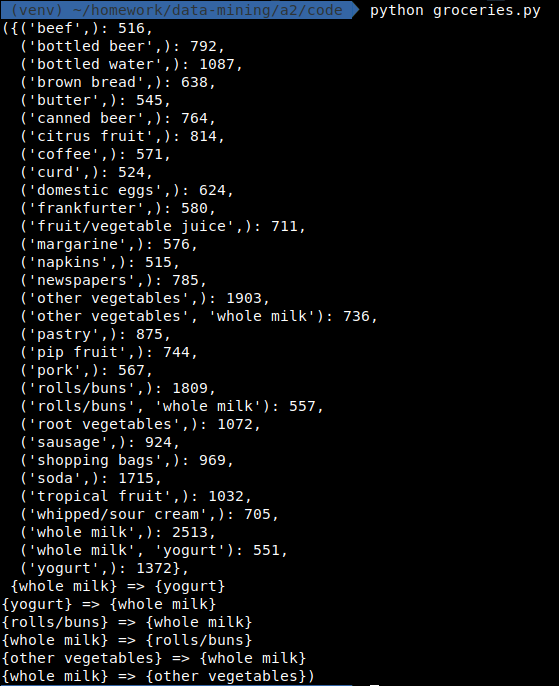
Unix storage
在最小支持度 0.15, 最小置信度 0.8 情况下
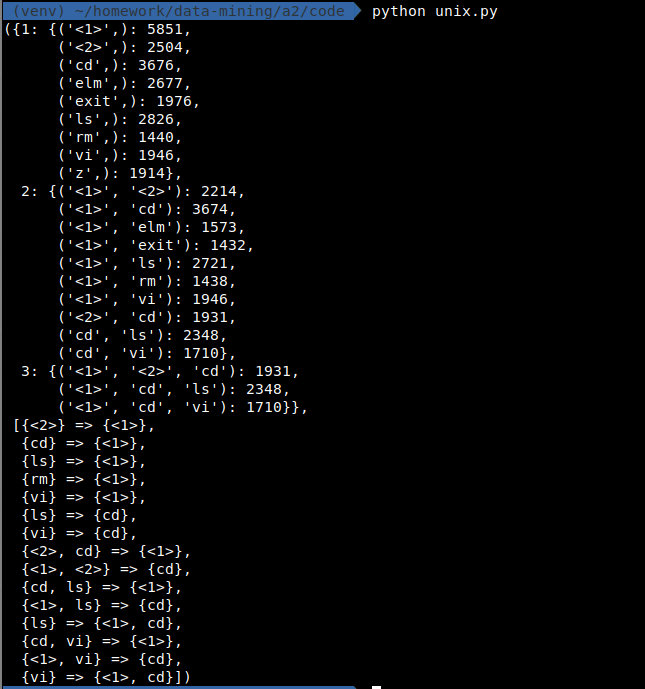
分析
首先一定有: 不同的算法虽然实现不同, 但其结果一定是相同的.
同样对 Unix storage 数据使用两种算法进行分析.
使用 Apriori, 时间开销 271 ms:
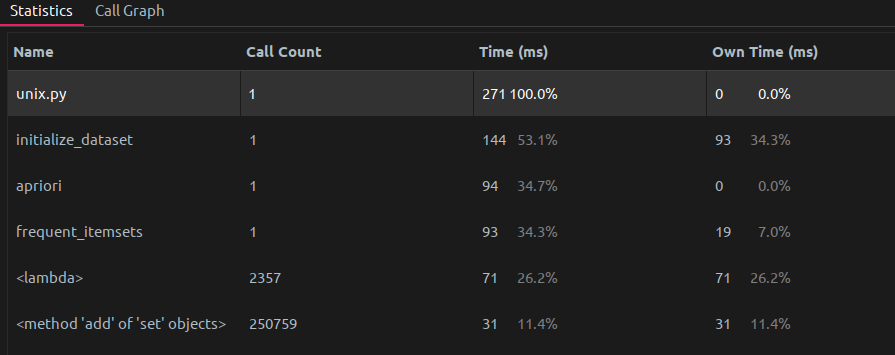
使用 FP-Growth, 时间开销 409 ms:
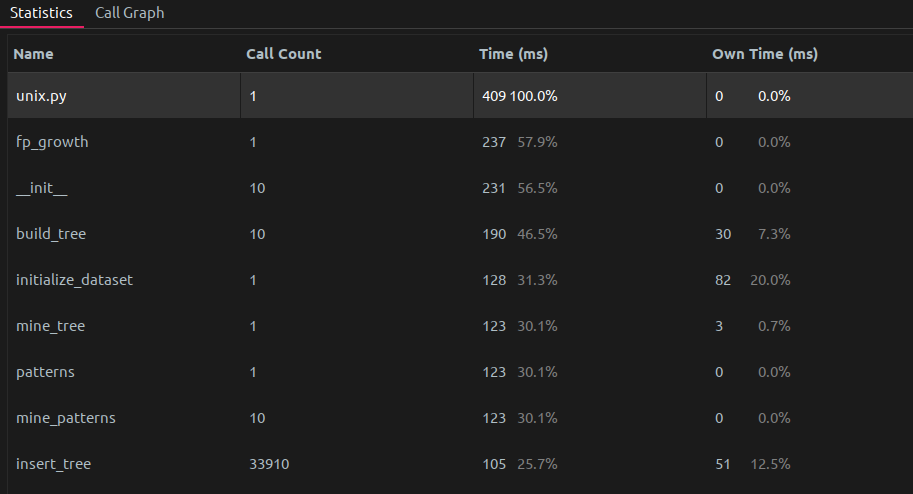
使用 dummy 方法, 时间开销令人震惊的只有 286 ms. 我的 dummy 算法改自 Apriori 算法, 即将其中剪枝的过程去除. 由于这一算法继承了 Apriori 中 bitarray 的优秀设计, 所以时间复杂度也很好.
这一表现其实与预期的 apriori 算法的时间复杂度比 fp-growth 要高不符
但需要指出, Apriori 算法中我进行了优化: 即将查找当前项是否满足最低支持度转化为了使用 bitarray 进行计算(因为最初的版本效率过低), 才能够将时间复杂度提高到与 FP-Growth 算法时间开销基本相同, 因此依然可以得出结论, 即 FP-Growth 的时间复杂度在理论层面一定是比 Apriori 高的
总结
(如果没有本次实验中的对应优化) 传统 Apriori 算法的时间复杂度确实非常之低, 而 FP-Growth 算法通过空间换时间, 通过建树与一些先验知识对频繁项集的提取进行了简化, 提高了算法的效率.
不过通过一些优化(见上文的算法介绍部分), 能够从另一个角度将原有的 Apriori 算法优化到我们可以接受的程度.