并行排序
概览
语言的选择
最初使用 Java 1.8.0_232 进行开发,但尤其是快排时,设置 threshold 后并发效率仍然和串行有一个数量级的差距,认识到 Java 线程切换的速度实在太不理想,考虑到我对 Java 运行机制的效率了解甚少,很难进行优化。听过老师的答疑后,决定最终以 C++ 实现。Java 版本代码仍然保留提交(code/java),只不过总体来看效率完全不理想,并行与串行相差一个数量级。
编译/运行环境
- Kernel: x86_64 Linux 4.19.88-1_MANJARO
- CPU: Intel Core I7-8550U @8x 4GHZ
- g++ 9.2.0
- cmake 3.16.0
cd code/cpp
mkdir build && cd build
cmake -DCMAKE_BUILD_TYPE=Release .. && make && ./parallel
技术要点
众所周知,std::sort 使用了 Introspective Sort 的平均效率较高,在实验中使用 std::sort 作为对照。
为了避免单词实验时的偏差,多次重复计算减少误差,重复次数在 main.cc 中定义宏 #define REPEAT 20,这一数值能够较好的平衡每次实验的时间和准确性。
由于线程相关的开销在数据量较小时可能会极大地影响实验结果,因此在 sort.h 中定义宏 #define BUCKET 1 将原有的数据重复 BUCKET 次放入数组。由于枚举排序的效率较低,当数据量较大时计算速度过慢,因此不会调整这一值。
快速排序
对于平凡的快速排序,使用了最方便的:
- 以最后一个值作为
pivot,进行partition; - 使用递归的方式重复调用。
对于并行快速排序,最开始的伪代码如下:
注:pid call 为并发调用函数,swap 与 C++ std::swap 语义一致
procedure partition(arr, low, high)
begin
pivot = arr[high], i = low - 1
for j = low to high - 1
if arr[j] < pivot then
++i
swap(arr[i], arr[j])
end if
end for
swap(arr[i + 1], arr[high])
return i + 1
end
procedure para_sort(arr, low, high)
begin
if low >= high then
return
end if
mid = partition(arr, low, high)
pid call para_sort(arr, low, mid - 1)
para_sort(arr, mid + 1, high)
end
通过实验可知,面对这样计算密集型的程序,创建的线程过多,程序时间的开销被大量浪费在线程的创建、切换、销毁,从这里我再次认识到,应该尽量减少线程开销,充分利用有限的核。
想到以下两种方式:
- 设置 threshold,然而这一参数过于具有人为性质,且在有不同 CPU 的计算机上的 performance 相差较大。
- 使用
atomic_uint维护可用的核数。然而当线程数变多时,同步的代价也会变得比较高昂。
决定:鉴于核数一般为 2 的幂,函数参数中维护 depth 变量,从 2 开始,每层 depth <<= 1,如果有 8 核,当 depth <= 8,经过 2, 4, 8 三层,函数会分为 8 个线程进行计算,可以比较有效的利用所有的线程。
不过,经过实验发现,depth 从 1 开始的效率能够更高,究其原因,我认为不同的线程并不会同时开始或结束,因此在计算过程中常会有空闲的计算资源。而线程翻一番的情况下,能够更好地利用所有的计算资源,带来的收益大于线程的开销。
伪代码如下,计算时间复杂度为 $O(2n \cdot (1 - \frac{1}{2^{log_2p}}) + \frac{n}{p} \cdot log\frac{n}{p})$
注:hardware_concurrency() 与 C++ std::thread::hardware_concurrency() 语义一致,在运行期获得硬件支持的并行数量
num = hardware_concurrency()
procedure para_sort(arr, low, high, depth=1)
begin
if low >= high then
return
end if
mid = partition(arr, low, high)
if depth <= num then
pid call para_sort(arr, low, mid - 1)
para_sort(arr, mid + 1, high)
else
sort(arr, low, mid - 1)
sort(arr, mid + 1, high)
end if
end
枚举排序
平凡的枚举排序的总复杂度为 $O(n^2)$,并行 $p$ 多处理器的枚举牌序的计算复杂度也只能为$O(\frac{n^2}{p})$。
并行枚举牌序的初版伪代码如下
注:len 函数与 Python len 函数一致,获取容器的元素个数
src = array[n] 在堆上初始化 src 为长度为 n 的数组
procedure rank(arr, v)
begin
count = 0
for value in arr
if v > value then
++count
end if
end for
return count
end
procedure para_sort(arr)
begin
num = hardware_concurrency()
src = array[len(arr)]
swap(src, arr)
for p = 0 to num - 1 par-do
i = p
while i < len(arr)
arr[rank(src, src[i])] = src[i]
i += num
end while
end for
end
但在这种情况下,当数组较大时,对于每个线程来说,i 每次步进 num 可能会导致 cache 命中率降低,基于此进行了改良,将整片数组按区域分为多份,保证 cache 命中率
procedure para_sort(arr)
begin
num = hardware_concurrency()
src = array[len(arr)]
swap(src, arr)
bucket_num = len(arr) / num + (len(arr) % num > 0)
for p = 0 to num - 1 par-do
i = bucket_num * p
while i < bucket_num * (p + 1) and i < len(arr)
arr[rank(src, src[i])] = src[i]
++i
end while
end for
end
归并排序
归并排序本可以按照快速排序的死路一样进行分治,为了更好地提高效率,使用了均匀划分技术,伪代码较长,分几部分展示来更好地体现死路。
平凡的归并排序
procedure merge(v, ll, rl, rh, dst)
begin
lh = rl, i = 0
while ll < lh && rl < rh
dst[i++] = v[ll] < v[rl] ? v[ll++] : v[rl++]
end while
while ll < lh
dst[i++] = v[ll++]
end while
while rl < rh
dst[i++] = v[rl++]
end while
end
procedure sort(v, n)
begin
dst = array[n]
seg = 1
while seg < n
p = 0
while p < n
ll = p, rl = min(n, p + seg), rh = min(n, rl + seg)
merge(v, ll, rl, rh, dst + ll)
p += 2 * seg
end while
seg <<= 1
copy all elements from dst to v
end while
以上代码使用迭代而非递归的方式进行平凡的归并排序
均匀划分技术
procedure para_sort(arr)
begin
num = hardware_concurrency()
// 0. divide evenly
bucket_num = len(arr) / num + (len(arr) % num > 0)
sample = array[num * num]
for p = 0 to num - 1 par-do
front = bucket_num * p
actual_bkt_num = min(bucket_num, len(arr) - front)
// 1. partial sort
sort(arr + front, actual_bkt_num)
split_num = actual_bkt_num / num + (actual_bkt_num % num > 0)
// 2. regular sampling
for j = 0 to num - 1
sample[num * p + j] = arr[front + min(actual_bkt_num, j + split_num]
end for
end for
// 3. sort sample numbers
sort(sample, num * num)
// 4. select pivots from sample
pivots = array[num - 1]
for i = 1 to num - 1
pivots[i - 1] = sample[i * num]
end for
marker = array[num][num + 1]
for p = 0 to num - 1 par-do
front = bucket_num * p
actual_bkt_num = min(bucket_num, len(arr) - front)
// 5. divide by pivots and record position to marker
j = 0
marker[p][j++] = front
while arr[front] > pivots[j - 1]
marker[p][j++] = front
end while
i = front
while i < front + actual_bkt_num and j < num
while arr[i] > pivots[j - 1] and j < num
marker[p][j++] = i
end while
++i
end while
while j <= num
marker[p][j++] = front + actual_bkt_num
end while
end for
// mark the border of every block to sort and record them to border
border = array[num + 1]
border[0] = 0
count = 0
for j = 1 to num - 1
for i = 0 to num - 1
count += marker[i][j] - marker[i][j - 1]
end for
border[j] = count
end for
border[num] = len(arr)
src = array[len(arr)]
swap(src, arr)
for p = 0 to num - 1 par-do
k = border[p]
// 6. globally move elements between blocks
for i = 0 to num - 1
length = marker[i][p + 1] - marker[i][p]
for j = marker[i][p] to marker[i][p + 1] - 1
arr[k + 1] = src[j]
end for
end for
// 7. partial sort in block
sort(arr + border[p], border[p + 1] - border[p])
end for
end
上边的方法严格按照均匀划分技术,注释中说明了每步的位置。
之后发现了其中的一部分问题在于:最后一次块内排序完全没有必要重新排序,由于每个块内都由 n(处理器数)个已排好序的块分配而来,因此,只需要对这 n 个部分进行 n - 1 次归并即完成。
如此以来,并行归并排序的计算复杂度为 $O(\frac{n}{p}\cdot log(\frac{n}{p}) + log_2p \cdot \frac{n}{p})$
这样的基于给定块边界进行归并排序的函数,使用了简单的状态机的思路:每三个边界的标记点完成一次状态机的循环。伪代码如下,在我的源代码中使用了重载,因此函数名相同。
procedure sort(v, gap, n)
begin
src = array[gap[n - 1]]
enum Status {left, mid} status
flag = array[n] of bool
init all elements of flag to be true
while true
ll = 0, rl = 0, rh = 0, count = 0
status = left
copy all elements from v to src
for k = 0 to n - 1
if !flag[k] then
continue
end if
if status == left then
flag[k] = false
status = mid
rl = gap[k]
else
rh = gap[k]
merge(src, ll, rl, rh, v + ll)
++count
ll = rh
status = left
end if
end for
if count == 0 then
break
end if
end while
end
对均匀划分的函数修改部分只涉及到最后一次的并发 par-do。
src = array[len(arr)]
swap(src, arr)
for p = 0 to num - 1 par-do
gap = array[num]
k = border[p]
for i = 0 to num - 1
length = marker[i][p + 1] - marker[i][p]
for j = marker[i][p] to marker[i][p + 1] - 1
arr[k + 1] = src[j]
end for
gap[i] = k - border[p]
end for
sort(arr + border[p], gap, num)
end for
运行时间
结果
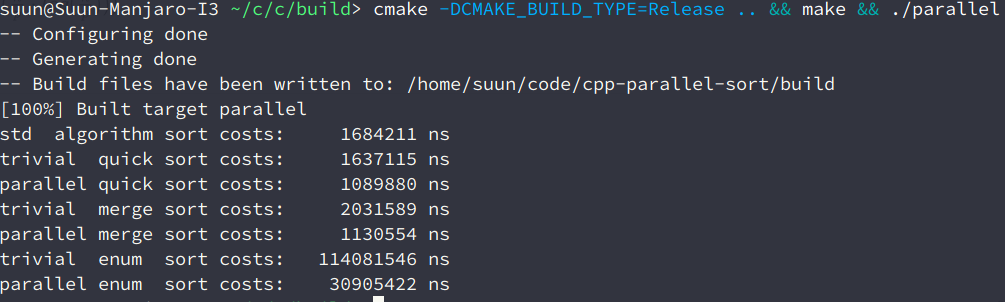
| 方法 | 串行 | 并行 |
|---|---|---|
| 快速排序 | 1,637,115 ns | 1,089,880 ns |
| 归并排序 | 2,031,589 ns | 1,130,554 ns |
| 枚举排序 | 114,081,546 ns | 30,905,422 ns |
$n = 30000, p = 8$
| Method | Time |
|---|---|
| std::sort | 1,684,211 ns |
| 串行快速排序 | 1,637,115 ns |
| 并行快速排序 | 1,089,880 ns |
| 串行归并排序 | 2,031,589 ns |
| 并行归并排序 | 1,130,554 ns |
| 串行枚举排序 | 114,081,546 ns |
| 并行枚举排序 | 30,905,422 ns |
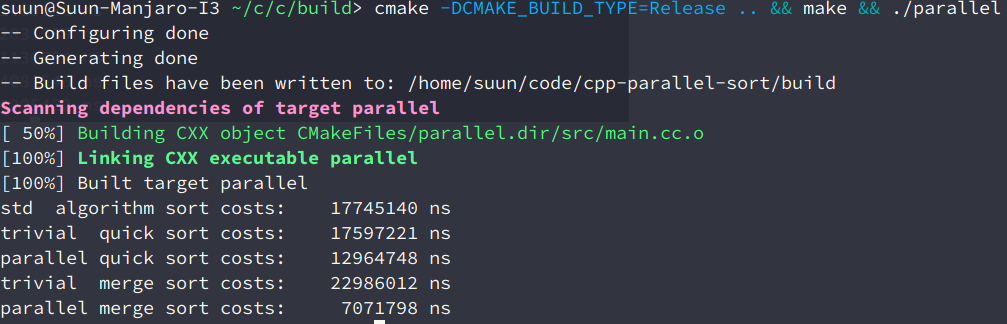
$n=30000 \cdot 10, p=8$
由于枚举排序太慢了,不参与本次运行时间统计。
| Method | Time |
|---|---|
| std::sort | 17,745,140 ns |
| 串行快速排序 | 17,597,221 ns |
| 并行快速排序 | 12,964,748 ns |
| 串行归并排序 | 22,986,012 ns |
| 并行归并排序 | 7,071,798 ns |
分析
首先再次强调使用 std::sort 进行对照的必要性:验证排序的耗时数量级正常,验证并行算法相比确实有提升。需要注意的是,在这里 std::sort 相比快排较慢的原因可能时因为 cmake 的 Release 开启的编译器优化为 O3 仍不足以使 std::sort 完全发挥,不过表现稍微差一点对我们的实验分析不造成影响。
因为 pivot 的选取恰巧不错且归并排序有一些时间开销浪费在复制数组上,串行快排的耗时相比串行归并较快。
并行算法都在原有串行算法的基础上相对不错的提高,而相同的程序在 JVM 上运行的提升却不理想,这是我不得不选择 C++ 的原因之一。
并行枚举排序理论计算复杂度为 $O(\frac{n^2}{p})$,然而耗时大概只减少到了 $\frac 1 4$,可见线程的开销在这次实验中数据较小的排序算法上难以让人忽视。
在数量较小时,并行快排相比并行归并稍微快一些,而在数量调大一个数量级后,并行归并的效率相比并行快排就好了很多。最根本的原因是,并行快排在最开始的几层节点中,并没有完全的发挥出多核的性能,而并行归并大部分时间都在全量发挥多核的计算能力。