Canny 边缘检测与内边界追踪

Apr 30, 2019

对目标图片进行边缘检测与边缘连接

原理

Canny 边缘检测算法与边缘连接/ Inner boundary tracing 的算法过程如下.

高斯滤波

使用高斯滤波矩阵作用于图像, 用以平滑图像来消除噪点.

梯度值与方向

使用 Sobel 算子 (或 Roberts, Prewitt 等), 分别得到横向与纵向两个方向的梯度.

根据横向梯度 $g_x$ 和纵向梯度 $g_y$, 计算梯度值与梯度方向. $$ G = \sqrt{g_x^2 + g_y^2}\ \theta = arctan \frac{g_y}{g_x} $$

非最大值抑制

在穿过某个点的四个直线上, 分别与相邻的两个梯度值进行比较, 只有它比相邻梯度值都大时将其保留.

这样能够将比较多的梯度值简化为较少的边界.

双阈值过滤

使用双阈值对图片的梯度值进行过滤, 若大于较大阈值则认为是边界; 若小于较小阈值则认为不是边界; 若位于双阈值之间, 且有超过较大阈值的梯度值相邻, 则也认为是边界, 否则认为不是边界. 伪代码:

if (image(row, col) > higher_threshold or
    (image(row, col) > lower_threshold and
     neighbor_greater_than_higher_threshold(row, col))):
    image(row, col) = 1;
else
    image(row, col) = 0;

内边界追踪

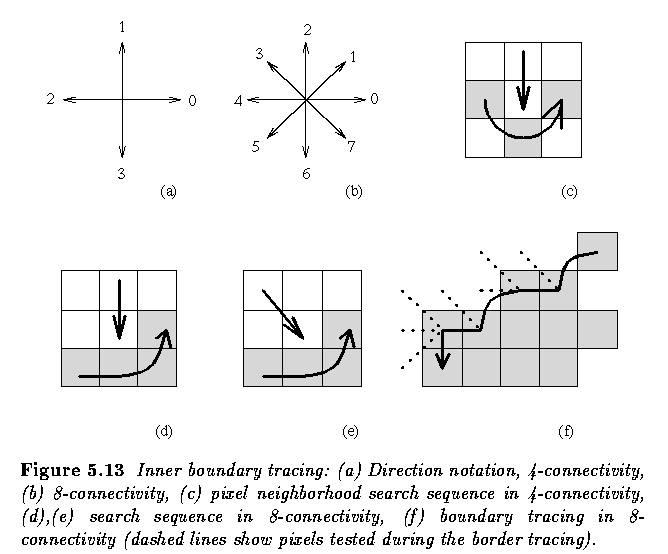
使用 Sobel 算子得到的图片有八连通边界, 以此为条件, inner boundary tracing 过程如下

设置初始 dir 为 7, 不同 dir 对应的方向如图 5.13(b);
逆时针搜索点的八近邻, 直到发现下一个边界点设为 dir, 且:
- dir = (dir + 7) % 8, if dir is even (图 5.13(d))
- dir = (dir + 6) % 8, if dir is odd (图 5.13(e))
搜索直到无法找到下一个边界点或回到起点.

细节

Canny 边缘检测算法在维基百科中的介绍已经非常全面了, 但一些实现细节仍需探讨.

频域上的变化

考虑到傅立叶变换后对高频空间进行过滤也能够有效地平滑图像, 因此考虑进行快速傅立叶变换之后, 将高频部分置为 0.

当然, 将低频部分过滤也可能起到非常好的作用, 但难以使用同样的指标对不同图片都进行低频过滤, 因此放弃过滤低频.

双阈值的取值

维基百科并没有对双阈值的取值给出准确的推荐值, 根据 Quora: How to set the threshold in canny edge detection, Stackoverflow: Canny edge detector threshold, 认为有两种对双阈值取值的方法.

根据 Lab Book Pages: Otsu Thresholding 计算 OTSU 阈值作为高阈值, 并取其 1/2 作为低阈值.
原灰度图平均值的 1.33 倍作为高阈值, 0.66 倍作为低阈值.

经过实践, 认为第二种方法的效果会更好并更具有可控性. 两种算法在代码中都有体现.

效果

Pic A

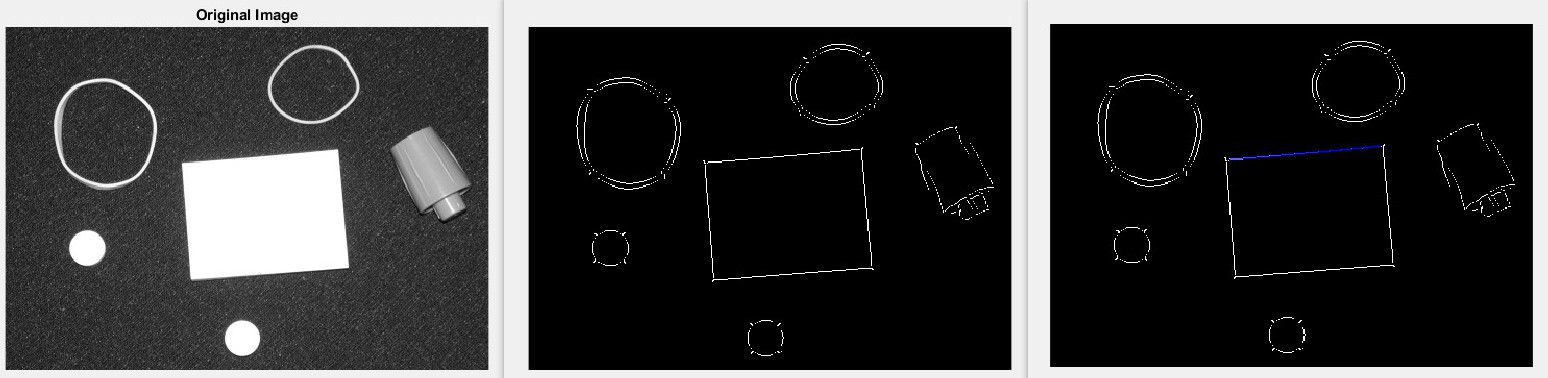
Pic B

实现

完整代码: edge_detection.m edge_linking.m

高斯滤波

高斯滤波在 MatLab 中可以通过 imfilter 实现.

function gauss_ret = gauss_blur(gauss_img)
    filter_matrix = 1/159 * [
        2 4 5 4 2;
        4 9 12 9 4;
        5 12 15 12 5;
        4 9 12 9 4;
        2 4 5 4 2];
    gauss_ret = imfilter(gauss_img, filter_matrix);

梯度值与方向

使用 Sobel 算子也可以使用 imfilter 函数. 在计算出 $\theta$ 后, 为了避免 nan 引入的问题, 将这些地方设为 2.

function [sobel_g, sobel_theta] = sobel(sobel_img)
    sobel_x = [-1 0 1; -2 0 2; -1 0 1];
    sobel_y = [1 2 1; 0 0 0; -1 -2 -1];
    x_ret = imfilter(sobel_img, sobel_x);
    y_ret = imfilter(sobel_img, sobel_y);
    sobel_g = sqrt(x_ret.^2 + y_ret.^2);
    sobel_theta = atan(y_ret./x_ret) * 180 / pi;
    sobel_theta = round(sobel_theta / 45) * 45;
    sobel_theta(isnan(sobel_theta)) = 2;

非极大值抑制

非极大值抑制只需要在四个方向上进行比较并拷贝. 为什么需要拷贝而不是在原图上操作? 避免在原图上的新结果影响最终的结果值.

edge = zeros(height, width);
for i = 2 : height - 1
    for j = 2 : width - 1
        if (...
            (abs(theta(i, j)) == 90 &&...
            g(i, j) >= g(i+1, j) &&...
            g(i, j) >= g(i-1, j)) ||...
            (theta(i, j) == 0 &&...
            g(i, j) >= g(i, j + 1) &&...
            g(i, j) >= g(i, j - 1)) ||...
            (theta(i, j) == 45 &&...
            g(i, j) >= g(i + 1, j + 1) &&...
            g(i, j) >= g(i - 1, j - 1)) ||...
            (theta(i, j) == -45 &&...
            g(i, j) >= g(i + 1, j - 1) &&...
            g(i, j) >= g(i - 1, j + 1))...
        )
            edge(i, j) = g(i, j);
        else
            edge(i, j) = 0;
        end
    end
end

双阈值过滤

双阈值的取值设为平均值的 1.33 倍与 0.66 倍.

upper_thresh = 1.33 * mean_value;
lower_thresh = 0.66 * mean_value;
edge((lower_thresh < edge) & (edge < upper_thresh)) = 0.5;
edge(edge < lower_thresh) = 0;
edge(edge > upper_thresh) = 1.0;
edge = filter_low_thresh(edge);

在 filter_low_thresh 函数中, 遍历所有点的八近邻, 如果当前点小于较大阈值大于较小阈值, 八近邻中有点大于较大阈值, 则视为边界.

内边界追踪

由于要将数字 0-7 转化为 8 个方向, 代码比较冗长, 因此这里省略部分代码.

在这部分, 需要明确:

什么时候终止继续寻找边界, 回到起点或找不到下一个边界点
MatLab index 值为 1-8, 需要进行转换

output = [row col;];
image(row, col) = 0;
dir = 7;
while (1)
    [row, col, next_found, dir] = find_next_dir(row, col, dir, image);
    if (~next_found)
        break;
    end
    if (output(1, 1) == row && output(1, 2) == col)
        break;
    end
    image(row, col) = 0;
    output = [output; row col;];
end

function [frh, frw, frfound, frp] = find_next_dir(fh, fw, fdir, fimage)
    [height, width] = size(fimage);
    signs = zeros(1, 8);
    # ...
    # set signs
    # ...
    frfound = 0;
    frp = mod(fdir + 1, 8) + 1;
    while (1)
        if (signs(frp))
            frfound = 1;
            break;
        end
        frp = mod(frp, 8) + 1;
        if (frp == mod(fdir + 1, 8) + 1)
            break;
        end
    end
    # ...
    # set return frh & frw
    # ...
    frp = frp - 1;
    if (mod(frp, 2) == 1)
        frp = mod(frp + 6, 8);
    else
        frp = mod(frp + 7, 8);
    end

参考资料

Lab Book Pages: Otsu Thresholding

Quora: How to set the upper and lower threshold in canny edge detection

Stackoverflow: Canny edge detector threshold

Wiki: Canny edge detector

Wiki: Sobel detector

Border Tracing